This is toward my understanding of the phrase “Why is height so important as an invariant? Because the height of a formal group law comes from the symmetry of the underlying variety.” In short — high amount of symmetry in the underlying abelian variety implies a high height of its formal group law (the converse is NOT true, if this was true, Elkies’s supersingularity theorem would be false).

One method of getting lower dimensional formal group laws from abelian varieties of higher dimension is via using the theory of complex multiplication — splitting the abelian variety by splitting the prime (as I exposited in my paper here).

I show that for abelian varieties with CM, the height of the formal group law pieces are expressible as a formula in terms of the degree of some field extensions of \(Q_p\) (one corresponding to each prime living over \(p\)) and the dimension of the rational endomorphism ring of the variety as a \(Q\)-vector space.

This proof was made possible by a couple helpful and fabulous conversations with Yifeng Liu. All errors are mine and mine alone.

Notation:

• \(F\) is a formal group associated to a CM abelian variety \(A\).
• \(\pi = \pi_A\), the geometric Frobenius of \(A\)
• \(L := Q(\pi)\) with \([L : \mathbb{Q}] = e\)
• \(D := End^0(A)\) with \([D: L] = r^2\)
• \(\dim(A) = g = er/2\).
• \(L\) is the center of \(D\)
• Assume that \(\mathcal{O}_L \subset End(A)\) (which we may after replacing \(A\) by an isogenous abelian variety).
• Consider the set \(\Sigma^{(p)}_L\) of discrete valuations of \(L\) dividing the rational prime number \(p\)

---

Theorem:

1. the decomposition \( D \otimes \mathbb{Q}_p \) \( = \prod_{w \in \Sigma^{(p)}_L} D_w\) and \( \mathcal{O}_L = \prod \mathcal{O}_{L_w} \) gives a decomposition \( F = \prod_w F_w \)
2. The height of \(F_w\) equals \([L_w : \mathbb{Q}_p]\cdot\) r.

We see that part 2 is very interesting — we are expressing the height of the chunk of the p-divisible group in terms of the rank of the endomorphism ring of the variety.

---

We will prove this theorem by

1. first proving the theorem for p-divisible groups \(X\), (a known theorem from these notes), that is, replace \(F\) with \(X := A[p^\infty]\).
2. then we will prove CM varieties produce p-divisible groups whose height is concentrated in its connected component.

---

Proof (Part 1): Note that \(ht(X) = 2 \dim A = er\). There is an action of \(D = End(A) \otimes Q\) on \(X\).

By taking the Dieudonne module of X, we get a vector space \(D(X)\) over \(\mathbb{Q}_p\) with an action of \(D\). The vector space \(D(X)\) is of dimension \(ht(X)\).

\[D(X) = \prod_{w \in \Sigma^{(p)}_L} D(X_w)\]

---

Remark: I think of \(\Sigma^{(p)}_L\) as the splitting of the prime \(p\) in L. For example, this is not literally true, but one might think of \(L\) as \(\mathbb{Q}(\zeta_7)\) and \(\Sigma^{(2)}_L\) is then the lifts of the splitting of the polynomial defining \(\zeta_7\) when we tensor with the 2-adics. \(Q(\zeta_7) \otimes \mathbb{Q}_2 \simeq K_1 \times K_2\). I think of \(K_1\) as \(\mathbb{Q}_2(1+x+x^3)\) and \(K_2\) as \(\mathbb{Q}_2(1 + x^2 + x^3)\), though this is not true, those two polynomials are just the first stage of the Hensel lifting: \((1+x+x^3)(1 + x^2 + x^3) \equiv 1+x+x^2 +x^3 + x^4 + x^5 + x^6 \mod 2\).

---

There is an action of \(D_w\) on \(D(X_w)\) (that is, \(D(X_w)\) is a \(D_w\)-vector space), and indeed, since \(D_w\) is still an extension of \(L_w\), we can thus think of \(D(X_w)\) as an \(L_w\)-vector space.

Remark: Something I still have to check, is \(L_w\) still the center of \(D_w\)? Are centers preserved by tensoring with \(\mathbb{Q}_p\)?

Now, for \(D(X_w)\) to be an \(L_w\) vector space, \(\dim(D(X_w))\) must be a multiple of the degree of extension over \(\mathbb{Q}_p\). In other words, \(\dim(D(X_w)) = r_w[L_w : \mathbb{Q}_p]\) for some constant \(r_w\).

It remains to show that \(r_w = r\).

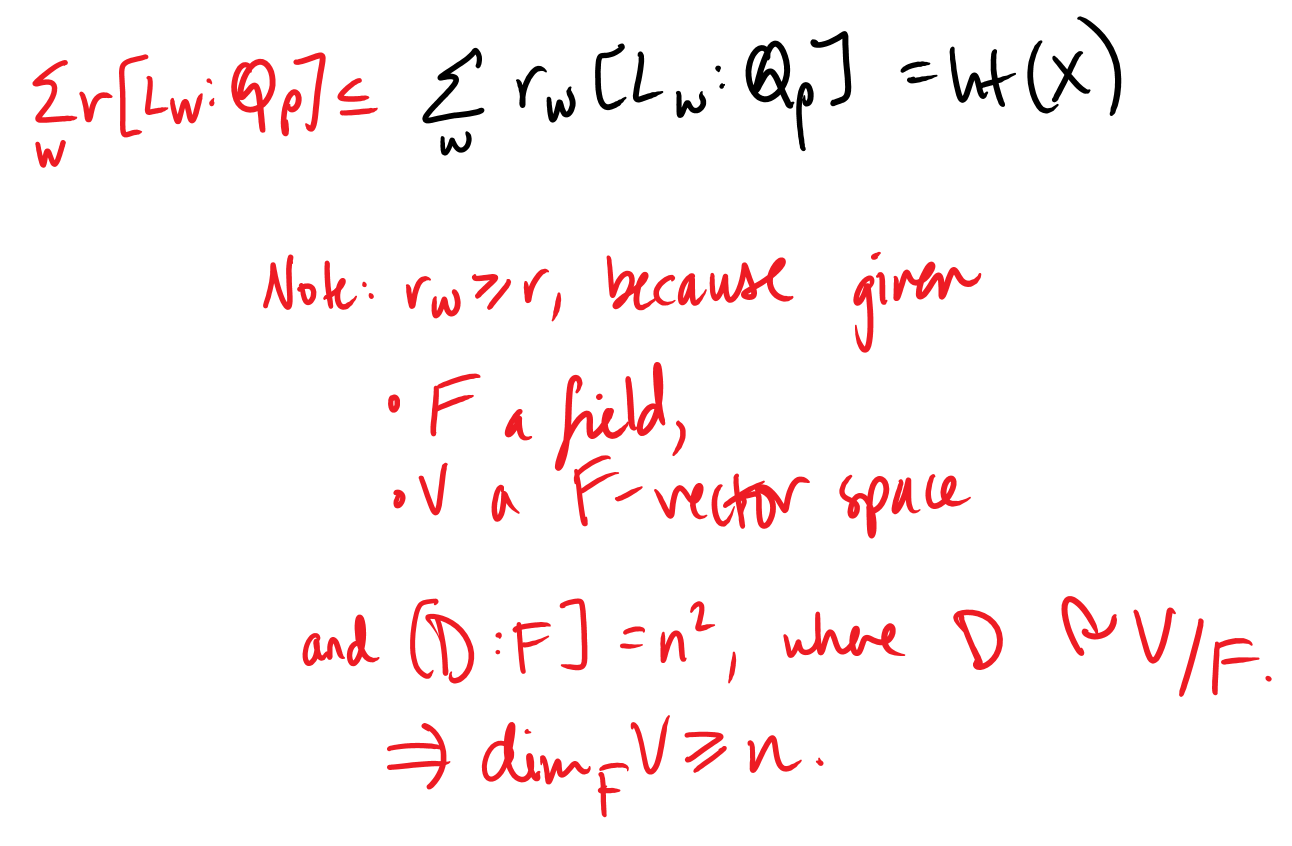
Thus: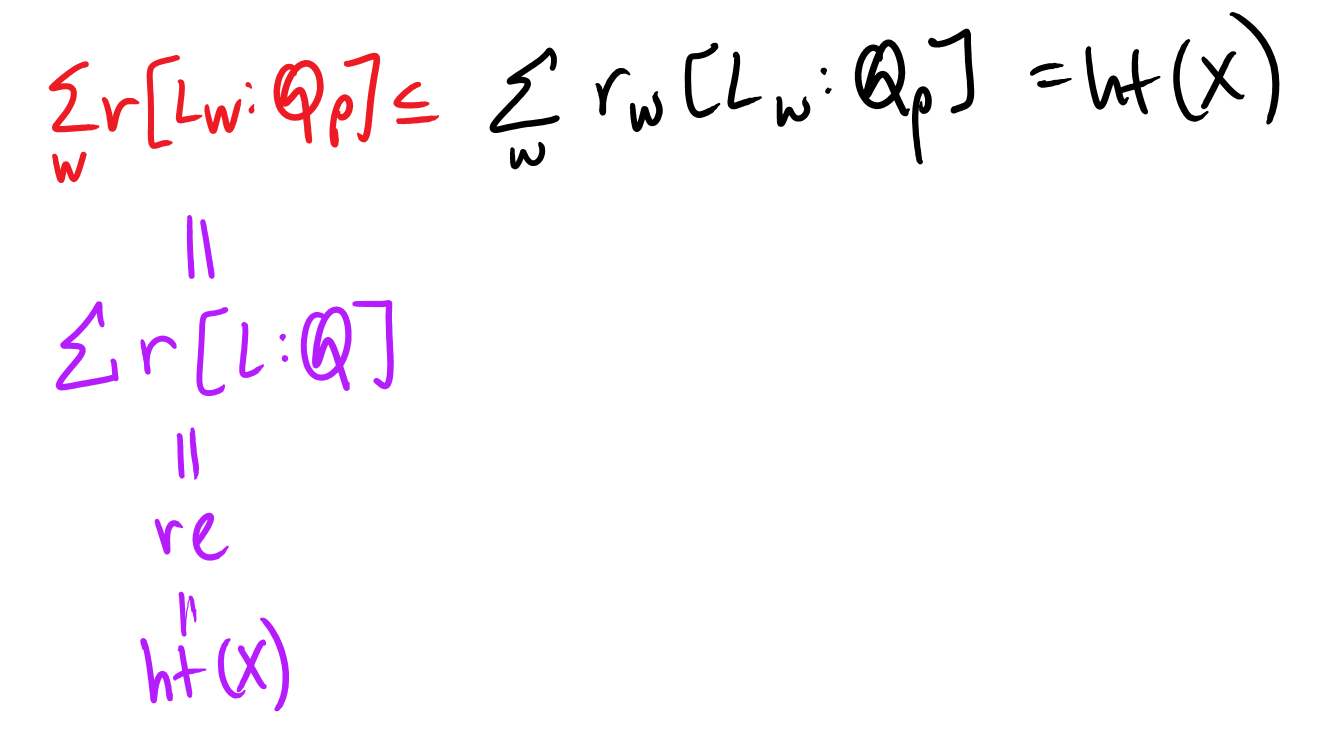

Therefore, \(r_w = r\). QED.

---

Why is this cool: Recall that \(r^2\) is the rank of the rational endomorphisms of the underlying abelian variety.

Now, we’ve proved it for the p-divisible group case. We may think of the formal group law as the connected component of the p-divisible group. Thus, we’ve also proved it formal group laws where the height of the p-divisible group is concentrated in its connected component.

Let us now show that CM varieties produce p-divisible groups whose height is concentrated in its connected component.

Proof (Part 2): For any abelian variety \(A\) (of genus \(g\)), we get the following short exact sequence in the category of group schemes over some field \(L\) such that \(L \simeq \overline{L}\) , for example \(L = \overline{Z_p}\) (algebraic closure):

\(0 \to A[p]^o \to A[p] \to A[p]^{et} \to 0\)

\(A[p]\) is a pointed scheme, and \(A[p]^o\) is the connected component in which this point sits. Further, \(A[p]\) is an Artinian scheme of length \(p^{2g}\).

Let \(\mathcal{O}_K\) be the ring of integers of the CM field \(K\) acting on our abelian variety \(A\) (note that \(K\) and \(L\) are different fields). Here we denote \(O_{K_p}\) as the ring of integers of \(K \otimes Q_p\). We know that \(\mathcal{O}_{K_p}\) acts on each of the components of the exact sequence.

We will show that \(A[p]^o(k) = F_{p^{2g}}\) when \(p\) is inert in \(O_K\) (that is, the height of the p-divisible group is concentrated in its connected component). When \(p\) is inert in \(O_K\), \(O_{K_p/p} \simeq F_{p^{2g}}\).

So, we have a few options: \(A[p]^{et}\) is either:

• Spec \(L\),
• or an Artinian scheme of length \(p\), \(p^2\), …, \(p^{2g}\).

We wish to eliminate all options to show that \(A[p]^{et} =\) Spec \(L\), which implies that \(A[p]^o\) is an Artinian scheme of length at least \(p^{2g}\).

We proceed as follows:

First, we see that if \(A[p]^o\) must be of length at least 1, that is, \(A[p]^o(L)\) cannot be Spec \(L\), it must be one of the following: \(F_p\), …, \(F_{p^{2g}}\).

Recall that \(A[p]\) is defined as the pullback of \(A \xrightarrow{p} A \leftarrow \text{ Spec }L\) in the category of group schemes. So, when we pull back \(p\) to \([p]*\), we see that \([p]* \not\simeq \text{Lie }A\) because \([p]_*\) acts as Fröbenius plus the Fröbenius transpose, and the Fröbenius acts as 0. So it cannot possibly be isomorphic to Lie \(A\).

So, now \(A[p]^{et}\) is either:

• Spec \(L\),
• or an Artinian scheme of length \(p\), \(p^2\), …, \(p^{2g-1}\).

Note that \(O_{K_p}\) contains \(Z\), and thus there is a \(Z\)-linear action on \(Ap\) where \(p\) acts as \(0\), so the action on \(E[p]^{et}(L)\) factors through \(O_{K_p/p} \simeq F_{p^{2g}}\).

An action of \(F_{p^{2g}}\) on \(F_{p^{2g-k}}\) is impossible for all \(k \geq 1\), and therefore \(A[p]^{et}(\overline{k})\) cannot be a Artinian scheme of length \(p^{2g-k}\) for \(k \geq 1\). Thus, \(A[p]^{et} \simeq \text{ Spec }L\):

\(0 \to A[p]^o \to A[p] \to \text{ Spec }L \to 0\)

Since \(A[p]\) is an Artinian scheme of length \(p^{2g}\), we conclude that \(A[p]^o\) is an Artinian scheme of length \(p^{2g}\).

Therfore, the height of the p-divisible group of an abelian variety with CM is the same as the height of its formal group law. QED.

---

So, that’s it! We’ve shown, for \(F\) a formal group associated to a CM variety:

1. the decomposition \( D \otimes \mathbb{Q}_p = \prod_{w \in \Sigma^{(p)}_L} D_w \) and \( \mathcal{O}_L = \prod \mathcal{O}_{L_w} \) gives a decomposition \(F = \prod_w F_w\)
2. The height of \(F_w\) equals \([L_w : \mathbb{Q}_p]\cdot \) r.