Hello. I don’t want much, just looking for a nice Variety to spend my days with. If you apply, I’d like you to have a well understood group law that comes from some 3-fold symmetry, but I’m a simple girl, easy to please, and I don’t need your group law to be all fancy and closed — a group chunk (group law which closed at least locally to the origin) is fine by me. I’ll have to put you through an interview process to see if you’re group chunk gives me a formal group law which is height 3, but don’t worry, it’ll be painless. Please let me know if you have a friend that matches this description!

This post is mostly a set-up to an (ill-formed) question. It’s motivated by this question:

How do I construct a variety which gives me a formal group law of height 3?

That is, I want it to have a nice kind of 3 fold symmetry which is reflected in its structure around a marked point.

I want this variety to not to be a bunch of copies of the additive or multiplicative group on (R^n). I am trying to define an at least 3-dimensional variety with a group chunk (that is, a group law which is closed at least locally to the origin). I want this group chunk to not be isomorphic to an additive, multiplicative, or elliptic group, or products of such groups.

The previous variety I was looking at ended up being isomorphic to the additive group, though it was very pretty. Aaron and a few others derived a variety from the relationship between the lengths of the vertices to a point interior to an equilateral triangle, which I rederived with the help of Laurens. Unfortunately the group law Alex Mennen and I defined on the variety ended up being the additive formal group law. I didn’t recognize it at first because it had 2 layers of square roots as a disguise, but Jack Shotton pointed out that if we did a variable change to get rid of the square roots (a variable change I had been doing formally to make calculations easier) it became quite obviously isomorphic to the additive group.

It was also pointed out to me by Doug Ravenel that height 3 formal group laws cannot be dimension 2. For some reason to do with the symmetry of the Jacobian of a dimension 2 variety which I don’t understand. So, I look now to dimension 3. More specifically, I look at tetrahedrons — the analogue of the square lattice, in some sense.

We begin with the vague desire of deriving a variety from some relationship on a tetrahedron (hoping that this variety has both a group law, and that the group law is height 3). Inna suggested that I look at a right angled tetrahedron to make my life easier, so we will look there.

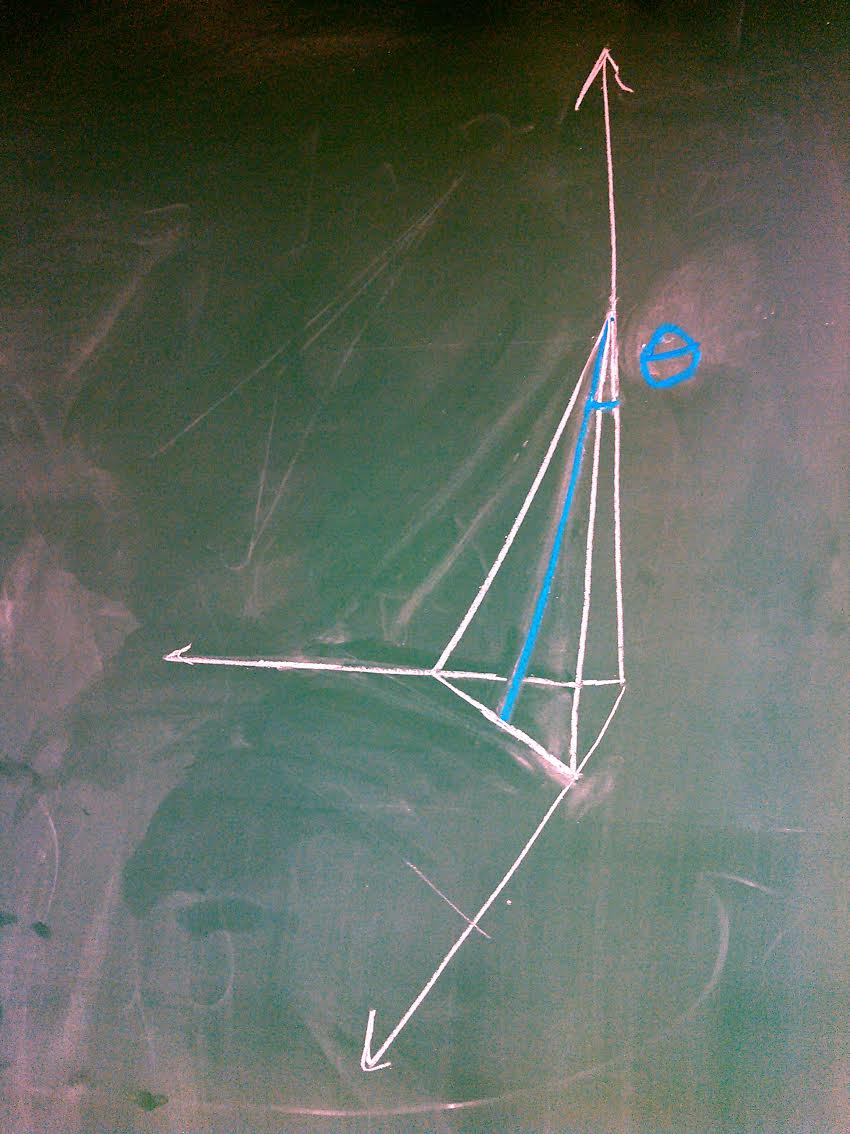
I had an idea for a group law on right-angled tetrahedrons: is a group in which each element is indexed by an angle, that is, the angle (theta) of the plane that intersects it symmetrically (to produce the tetrahedron).

Then, we might add their volumes. We now get a third volume. What is an angle which gives us a tetrahedron with this volume? Is it unique?

Inna and I talked about this and she referred me to a group law on angles of a tetrahedron, which looks multiplicative but involves (\sin), so perhaps is a bit more complicated. It looks something like this: (\alpha + \beta = \sin^2(\alpha)\sin^2(\beta)). Where does this group law live? What variety has angles as points? Does the free abelian group generated by tetrahedra have a geometric structure we could use?

Another issue: We now have a group law, but no variety! The whole point was to define a group law close to the origin, but what is closeness in this group?

I stop writing with a question still quite ill-formed and fuzzy:

How might we derive a variety based on a tetrahedron which allows us to put an angle-y/volume-y group law on its points?