This post is written together with Josh Mundinger. Last time, we compared the Harish-Chandra isomorphism \(Z(U\mathfrak g) \cong (\text{Sym} \mathfrak h)^{W,\cdot}\) for \(\mathfrak g= \mathfrak{sl}_2\) to the Duflo isomorphism \(Z(U\mathfrak g) \cong (\text{Sym } \mathfrak g)^{\mathfrak g} \cong (\text{Sym} \mathfrak h)^W\), and found that they differ exactly by a translation by \(\rho\). In this blog post, we study just the Harish-Chandra map \(Z(U\mathfrak g) \to \mathbb C[\mathfrak h]\), using the Fourier transform to explain why the image is invariant under the dot action \((W,\cdot)\). Recall that the Harish-Chandra map sends \(z \in Z(U\mathfrak g)\) to the action of \(z\) on the Verma module \(M_\lambda\). The dot action of \(W\) is defined by \(w \cdot \lambda = w(\lambda + \rho) - \rho\). Thus, for \(\mathfrak sl_2\), we need to show that the center of \(U\mathfrak sl_2\) acts by the same scalar on \(M_{\lambda}\)and \(M_{-\lambda - 2}\).

Twisted differential operators

The Beilinson-Bernstein localization theorem provides a geometric way to understand the universal enveloping algebra of a semisimple Lie algebra \(\mathfrak g\) through differential operators. For a smooth variety \(X/\mathbb C\), the sheaf of differential operators \(D_X\) on \(X\) is the sheaf of \(\mathbb C\)-linear operators \(\mathcal{O}_X \to \mathcal{O}_X\) which locally look like \[\sum_{i_1,\ldots,i_n} f_{i_1,\ldots, i_n} \frac{\partial^{i_1}}{\partial x_1^{i_1}}\frac{\partial^{i_2}}{\partial x_2^{i_2}}\cdots \frac{\partial^{i_n}}{\partial x_n^{i_n}},\] where \(f_{i_1,\ldots, i_n}\) are regular functions and \(x_1,\ldots, x_n\)are local coordinates. More generally, if \(\mathcal L\) is a line bundle on \(X\), then the sheaf of differential operators \(D^{\mathcal L}\) on \(\mathcal L\) is the sheaf of operators \(\mathcal L \to \mathcal L\) which look locally as above. This ring may be expressed in terms of \(D_X\) by the formula \[ D^{\mathcal L} = \mathcal L \otimes D_X \otimes \mathcal L^{-1} \] In our case, we are interested in \(X = \mathbb P^1 = SL_2/B\), the flag variety for \(SL_2\). Line bundles on \(\mathbb P^1\) are exactly \(\mathcal O(\lambda)\) for \(\lambda \in \mathbb Z\), and we will write \(D^{\lambda} = D^{\mathcal O(\lambda)}\).

It turns out that the algebra \(D^\lambda\) makes sense even when \(\lambda\) is not an integer! We have a map \[\pi: \mathbb{C}^2\setminus 0 \to \mathbb{P}^1.\] This is a quotient map for the action of \(\mathbb G_m\) by dilation on \(\mathbb C^2\). The derivative of the \(\mathbb G_m\)-action is given by the Euler vector field \[ eu = x_1 \frac{\partial}{\partial x_1} + x_2 \frac{\partial}{\partial x_2}\] where \(x_1\) and \(x_2\) are linear coordinates on \(\mathbb C^2\). In these terms, \[D^\lambda := (\pi_*D_{\mathbb C^2 \backslash 0}/(eu - \lambda))^{\mathbb G_m}.\] The above formula makes sense for any complex number \(\lambda\).The sheaf of rings \(D^\lambda\) is a sheaf of twisted differential operators on \(\mathbb P^1\).

Infinitesimal action and a Lemma of Beilinson-Bernstein

The theorem of Beilinson and Bernstein relates \(\mathfrak g\) to the flag variety \(X = G/B\). The line bundles on \(G/B\) are \(\mathcal O(\lambda)\) for \(\lambda\) a character of \(B/[B,B]\). In case \(G = SL_2\), then \(G/B = \mathbb P^1\), and \(\mathcal O(\lambda)\) for integer \(\lambda\) are the usual line bundles on \(\mathbb P^1\).

Lemma (Global Sections of D) If \(G\) is a semisimple complex algebraic group and \(X = G/B\) is the flag variety of \(G\), then \[\Gamma(X,D^\lambda) \cong U\mathfrak g/I_\lambda\] where \(I_\lambda\) is the ideal generated by the kernel of \(Z\mathfrak g\) on the Verma module \(M_\lambda\).

The map in this Lemma is induced by the infinitesimal action of \(G\)on \(X = G/B\). Given a path \(\gamma: (-\epsilon, \epsilon) \to G\) with \(\gamma(0)=1\), we obtain a family of automorphisms of \(X\); differentiating them gives a vector field on \(X\).This vector field depends only on \(\gamma’(0)\), and so we obtain a Lie algebra homomorphism \[ \mathfrak g \to \text{Vect}(X).\] In case \(G = SL_2\), \(X = \mathbb P^1\), we can calculate these operators on \(\mathbb C^2 \setminus 0\), then descend using the map \(\pi: \mathbb C^2 \setminus 0 \to \mathbb P^1\). Here are formulas for the infinitesimal action on \(\mathbb C^2 \setminus 0\):

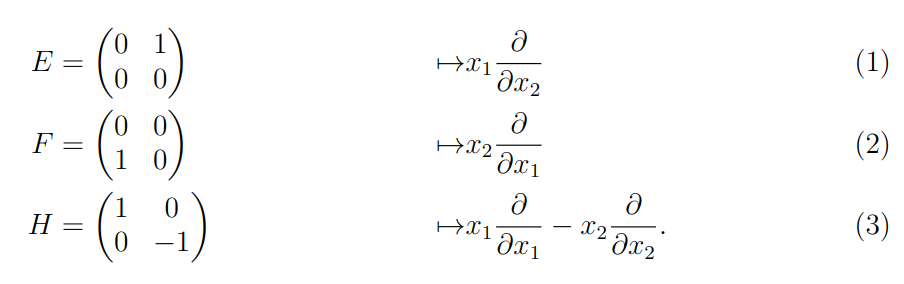
These formulas give a Lie algebra homomorphism \(\mathfrak{sl}_2\to \text{Vect}(\mathbb C^2 \setminus 0) \to D_{\mathbb C^2 \setminus 0}\), inducing a homomorphism of associative algebras \(U\mathfrak{sl_2} \to D_{\mathbb C^2 \setminus 0}\). The image of \(\mathfrak{sl_2}\) is \(\mathbb G_m\)-invariant since the action of \(SL_2\) commutes with dilation. So we get a ring homomorphism \[\mathrm{act}: U\mathfrak{sl}_2 \to D^\lambda = \pi_\ast(D_{\mathbb C^2 \setminus 0}/(eu - \lambda))^{\mathbb G_m}\] for all \(\lambda \in \mathbb C\). We have now given explicit formulas for the map in the Lemma above.

Fourier

In this section we show that the Fourier transform descends to an equivalence of categories between the category of \(D^\lambda\)-modules to the category of \(D^{-\lambda - 2}\)-modules for generic \(\lambda\). The Fourier transform naturally transforms differential operators on a vector space \(V\)to differential operators on the dual space \(V^*\).We show how this induces a map on twisted differential operators on \(\mathbb P^1\), where the \(\rho\)-shift will naturally appear.

Let \(V = \mathbb{C}^2\) with coordinates \(x_1,x_2\). On \( V^* \), we will use dual coordinates \((\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}) =: (y_1, y_2)\).Note that for \(\mathfrak g\) acting on a vector space \(V\), the action of \(x\in \mathfrak g\) on \(V^*\) is defined as \(x(v^*) = v^* \circ(-x)\). Thus, on the dual basis, we get the following action of \(\mathfrak{sl}_2\):

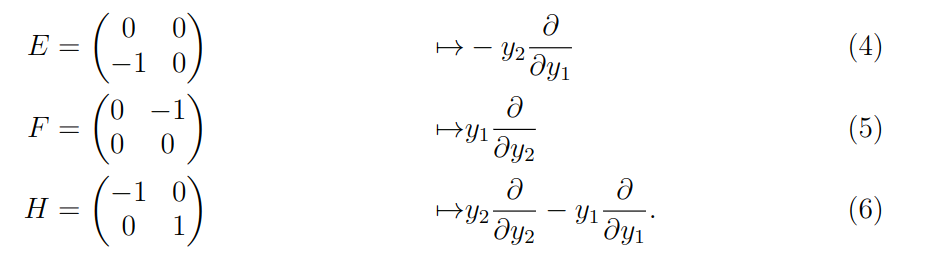
Note that these matrices are different than the ones we had before. In this basis, \(E\) acts by \(-F\) on the dual, \(F\) acts by \(-E\) on the dual, and \(H\)acts by \(-F\) on \(V^*\)

The Fourier transform \(\phi: D_V \to D_{V^*}\) is defined by \[ \phi(x_i) = \frac{\partial}{\partial y_i}, \quad \phi\left(\frac{\partial}{\partial x_i}\right) = - y_i.\] The goal of this section is to show that the Fourier transform \(\phi\) induces the following commutative triangle.

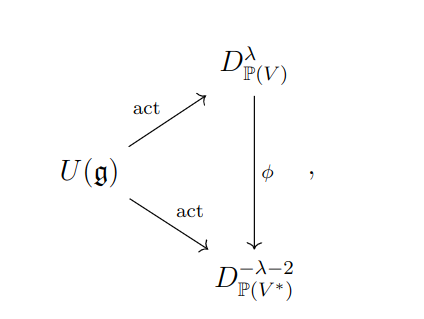
where \(\mathrm{act}\) is the infinitesimal action of the last section. This commutative triangle implies that the central character of \(\lambda\) is the same as the central character of \(-\lambda - 2\), which gives us that the Harish-Chandra homomorphism is invariant under the \((W,\cdot)\) action.

We begin by showing the vertical arrow is well defined by an explicit calculation with the Euler fields on \(V \)and \( V^* \): \[\phi (eu) = \sum_i (-\frac{\partial}{\partial y_i}y_i) = \sum_i (-y_i \frac{\partial}{\partial y_i}-1)= -eu - 2.\] Hence \( \varphi( (eu - \lambda)D_{V}) = \varphi( (eu - (-\lambda - 2))D_{V^*}) \). Now \(D_V\)and \(D_{V \setminus 0}\) are not the same, as the latter is a sheaf on the non-affine scheme \(V \setminus 0\). Nonetheless we get a map \[ \varphi: D_{V \setminus 0}/ (eu - \lambda)D_{V\setminus 0} \to D_{V^* \setminus 0}/ (eu - (-\lambda - 2)D_{V^* \setminus 0} \] and thus \(D^\lambda_{\mathbb P V} \to D^{-\lambda - 2}_{\mathbb PV^*}\).

To fill in the triangle, we need to check that \(\varphi\) intertwines the infinitesimal action of \(\mathfrak{sl}_2\) on \(V\) and \(V^*\). We calculated both of these earlier! The Fourier transform sends infinitesimal actions defined by equations (1), (2), (3) to (4), (5), (6) respectively. Thus we conclude the triangle commutes.

Central Characters

By the Lemma (Global Sections of D), this commutative triangle induces the following triangle on global sections:

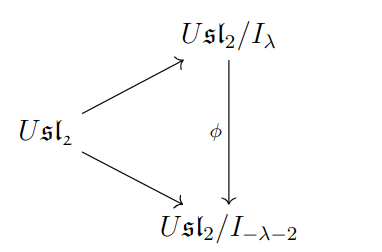
where \(I_\lambda\) is the ideal of the central character of \(\lambda\) under the Harish-Chandra homomorphism.

This shows that the Harish-Chandra homomorphism is invariant under \(\lambda \mapsto -\lambda - 2\), as desired.

The reason that the shift \(\lambda \mapsto -\lambda - 2\) shows up in today’s story comes from the Fourier transform of the Euler field. When the Fourier transform is treated in a more coordinate-free manner, the canonical bundle shows up. The canonical bundle of \(\mathbb P^1\) is \(\mathcal O(-2)\), and that \(-2\) is the same \(-2\) as in \(-\lambda - 2\). We will elaborate on this in the future.