I didn’t want to use a brute force method, so I thought for a while about how to compute the cup product of the Klein bottle. This is what I came up with. I thought I’d share it.

Take coefficients in \(\mathbb{Z}/2\). We compute the cup product by computing the intersection form (which defines the intersection product), then Poincare duality.

The Klein bottle is compact and \(\mathbb{Z}/2\)-orientable, so Poincare duality applies: \(a^* \smile b^* = [a.b][K]\)

where \([K]\) is the fundamental class of the Klein bottle, \([a.b]\) is the number of intersections of the cycles \(a\) and \(b\) (thought of as sub-manifolds embedded in the Klein bottle). Note that \(a^\) and \(b^\) denote the cocycles corresponding to the cycles \(a\) and \(b\) respectively.

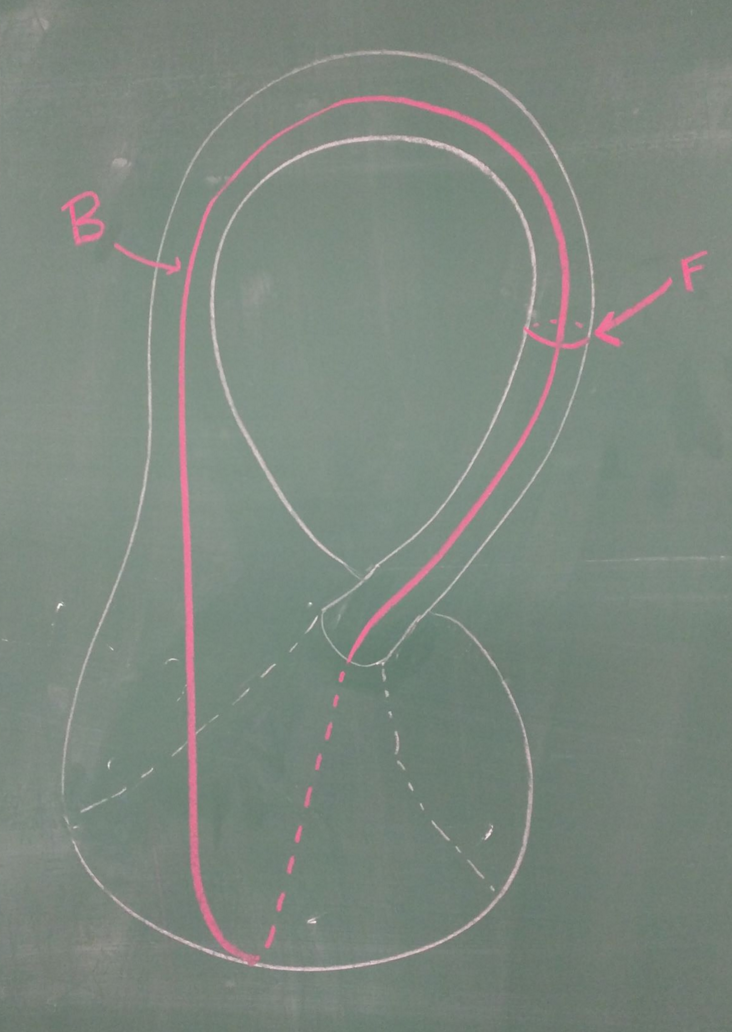
We view the Klein bottle as the fiber bundle \(S^1 \to K \to S^1\) Fix a fiber circle, \(F\), and denote the base circle as \(B\).

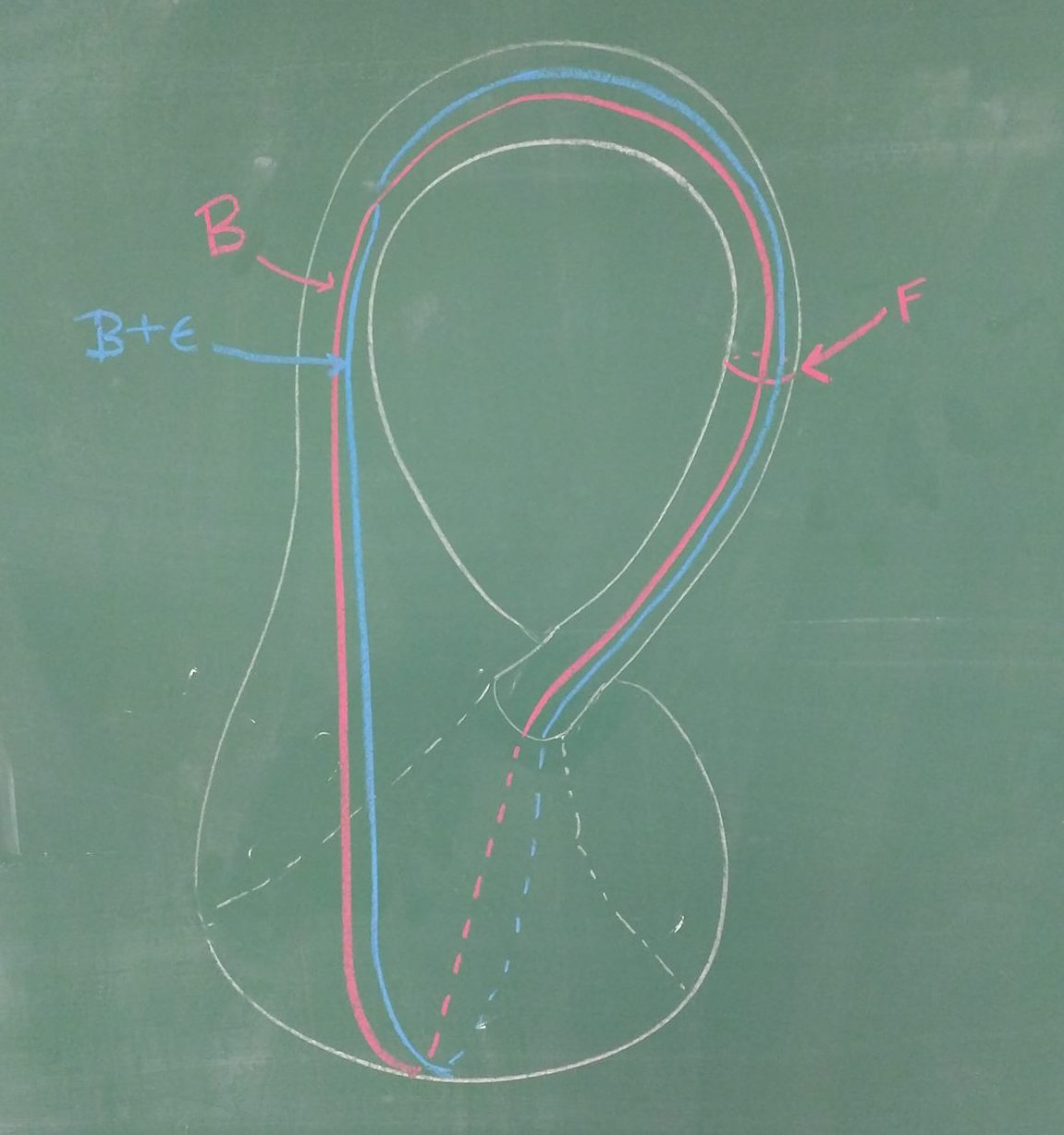
By pictoral argument: \(F\) has zero transverse intersection with itself and intersects the base circle \(B\) once. By wiggling the base circle by an infinitesimal amount \(\epsilon\), we see that \(B\) intersects transversely with itself once.

Another perspective:

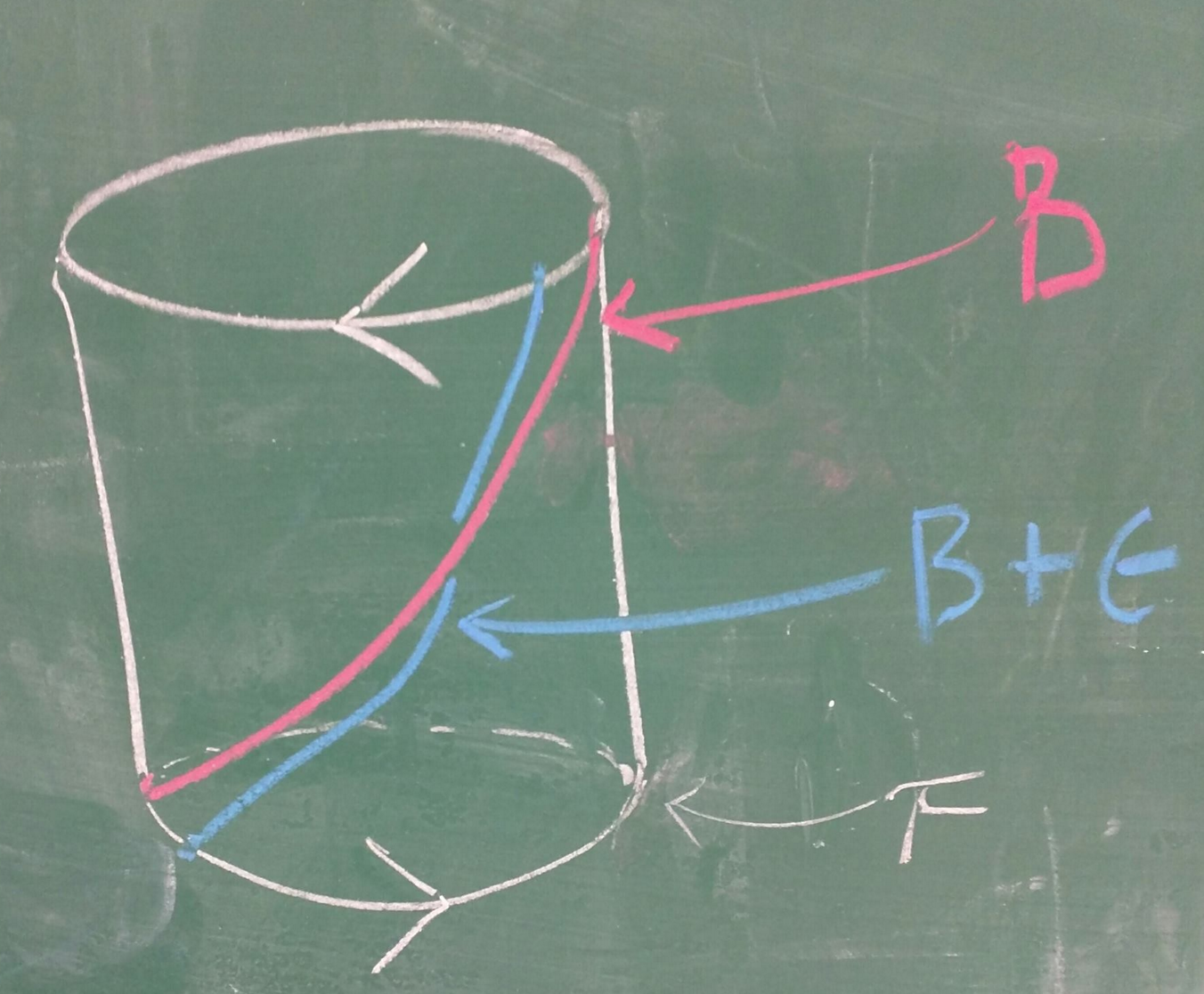
We may more succinctly state the intersection product as the following matrix:

\(\begin{pmatrix} \beta \smile \beta & \beta \smile \gamma \ \gamma \smile \beta & \gamma \smile \gamma \end{pmatrix} \simeq \begin{pmatrix} [B.B] & [B.F] \ [F.B] & [F.F] \end{pmatrix} = \begin{pmatrix} 1 & 1 \ 1 & 0 \end{pmatrix}\)

From the above matrix, we see that \(\beta^2 = \beta\gamma = 1[K]\), and \(\gamma^2 = 0[K]\). And, of course, \(\beta^3 = 0\), because \(H^3(K) = 0\). This gives us the ring structure of \(H^*(K; \mathbb{Z}/2)\): \((\mathbb{Z}/2\mathbb{Z})[\beta, \gamma]/(\beta^2 + \beta\gamma, \gamma^2, \beta^3)\)

P.S. If we wanted to be totally rigorous, we’d have to show that the cocycles \(\beta\) and \(\gamma\) form the basis of the \(H^1(K; \mathbb{Z}/2) \simeq \mathbb{Z}/2 \oplus \mathbb{Z}/2)\). Until then, we don’t quite have that the intersection matrix gives us the cup product of \(H^*(K; \mathbb{Z}/2)\).