I also work in chronic pain research. Before I was in math, I worked mostly in scientific simulation, autonomous robotics, and medical technology.

Here is a summary of my past non-math research and projects

(In construction, can be viewed on my github).  My first projects in robotics were in 2011: a dinky hexapod that autonomously followed people around, and Rubik's cube solving robot. In Spring 2012, I [became interested](http://rin.io/coupled-oscillator-love/) in physical examples of [nonlinear systems](http://rin.io/matlab-lorenz-attractor/) due to a [research project](http://thefutureofthings.com/4060-flexible-memristor-chips/) at the Chemistry and Physics Department of Mary Baldwin College, and modeled the resistant switching behavior of [flexible TiO2](http://books.google.com/books?id=Aey-h9lgcQgC&pg=PA111&lpg=PA111&dq=tio2+memristor+mary+baldwin&source=bl&ots=_Cxkt4ZyU8&sig=12ZG4phc_r1cNRkhmyg99YZ1dUc&hl=en&sa=X&ei=U0dcVN2RBdHToAT4u4LoDQ&ved=0CEMQ6AEwBQ#v=onepage&q=tio2%20memristor%20mary%20baldwin&f=false).  Summer 2012, the [Positronics Division of the George Washington University Robotics Lab](http://robotics.gwu.edu/positronics/?page_id=9) took me under their wing as an intern. Our team smoothed joint movement of the Willow Garage Personal Robot 2 (PR2), alongside improving load equalization (below). I [programmed the PR2](http://rin.io/semi-autonomous-robotics-2012-my-1st-software-project/) to autonomously "learn" to place objects in holes with the corresponding shape (using only past motor position commands and the finger gripper sensors).  [Source](http://robotics.gwu.edu/positronics/?p=59) On the side, fascinated by the phenomena of producing argon plasma glow via the introduction of an RF source at 2.45GHz to a conductive cavity, I modeled the modes of conductive [polyhedra](http://en.wikipedia.org/wiki/Goldberg_polyhedron)[.](http://robotics.gwu.edu/positronics/?page_id=9) After transferring to [GMU](http://rin.io/18-lessons/) Fall 2012, I extended their simulation for [predicting the material properties](http://rin.io/computational-materials-science/) of compound materials and explored [algorithms of AI chess players](http://rin.io/chess-engine/). Spring 2013, an interest in contextual machine learning led me to write an [automated contextual analysis program](https://github.com/catherineray/CAMEL) that [learned the grammar rules of compressed Braille](http://rin.io/camel-paper/) from partially translated text. I used Braille as a test language, but this is a framework to automate the decoding of any partially understood (ancient) language by creating probabilistic dictionaries.\ [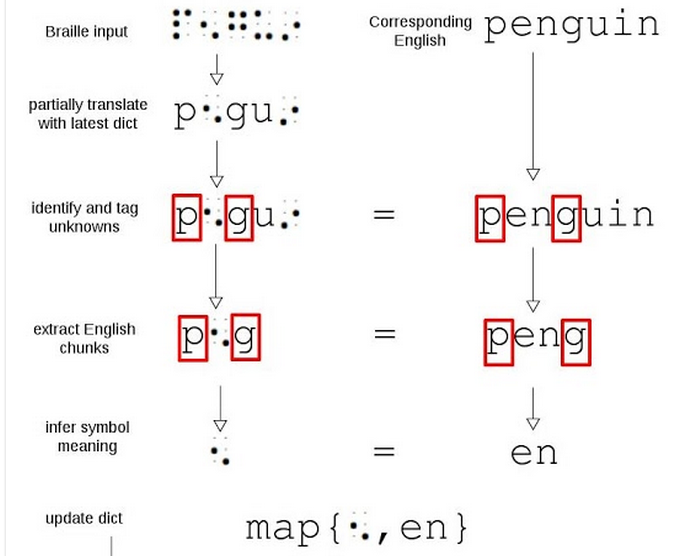 Summer 2013, I interned as a software engineer at Cloudera. During my time there, I [developed a consumer download metrics tracking system for internal purposes](http://blog.cloudera.com/blog/2013/08/what-i-learned-during-my-summer-internship-at-cloudera/). Fall 2013, I played with [SLAM and motion planning on the ARDrone](http://masc.cs.gmu.edu/wiki/DeformGroup). For HackMIT 2013, I collaborated with [Kartik Talwar](http://kartikt.com/) and [Spencer Hewett](http://www.skip.it/) to create a Google Glass application that [calculates the human pulse from the video feed](http://rin.io/hackmit-polyglass/).\ [ Early 2014, I briefly devoted my time to designing a keychain-sized food scanner [that detects gluten and other common food allergen proteins](http://rin.io/reframing-the-gluten-scanner/). From late 2013 to mid 2014, I dipped my toes into audio processing by automating the collection and classification of lab-animal vocalizations. Through this, I discovered that one can detect libido and stress change as early as preclinical trials. [](https://web.archive.org/web/20190213160322/http://rin.io/wp-content/uploads/2014/06/Screenshot-from-2014-06-21-194605.png)  Summer 2013-Spring 2014, I explored the improvement of mobility devices. A nonprovisional patent was submitted in Dec 2014 for the 5 pressure sore relief mechanisms that grew out of this. (I withdrew the patent once I decided to go into academia because I did not need to spend 5K on a design I wasn't going to use!) Summer 2014, I became interested in neuroprosthetics. I started with the software side (convergence analysis of common decoder algorithms), and transitioned into playing with the hardware side ([optical recording methods](https://web.archive.org/web/20190213160322/http://rin.io/sensing-hardware/)). Early 2015, I began mentoring Ada Rosa on mobility assistance for those with ALS and spinal chord injuries. [Here](https://www.youtube.com/watch?v=YJxgEDr699w) is a video of her showing off the eye control feature. In January 2015, I was a [visiting researcher](https://web.archive.org/web/20190213160322/http://www.santafe.edu/gevent/detail/arrival/1962/) at the Santa Fe Institute, and gave a seminar on [Simplifying Multiscale Modeling](https://web.archive.org/web/20190213160322/http://www.santafe.edu/gevent/detail/science/1963/). I still think about applications of topology to multi-scale modeling, and occasionally venture to consider modeling complex systems of a biological nature with an eye toward [immunotherapy](https://web.archive.org/web/20190213160322/http://www.infoiasi.ro/bin/Annals/Article?v=XXIV1&a=2) and [neuroscience](https://web.archive.org/web/20190213160322/http://xxx.tau.ac.il/pdf/1410.8826.pdf). I stopped keeping temporal notes of projects around 2015. Most of my extra curriculars post moving to math academia have been artistic or biological. I studied Russian from 2018-2020 and spent 4 months in Russia in 2019, the end of my trip was right at the beginning of Putin's violent crackdown on Moscow. I continue to do biological research on the side, especially around chronic pain and it's relationship to mental health. An overview of that work can be found here: [The Biome](https://rin.io/biome/) Over the period of 2021-2023, I collaborated with Chris Orta to design and tattoo two massive full robot-skeleton snakes going from the top of my back to my mid calf. In the summer of 2023, I got heavily into street art graffiti, learning from my artistic collaborator Daniel Burnett: some samples of my graffiti work can be seen in the art section of my webpage. I have traveled around the U.S. and Europe making graffiti since. In August 2023, I joined Chris Walker and a group of other fabulous artists to finish up and sail a boat made from a bouncy castle, which we lived on for a week. My dear friend Petra Flurin and I wrote a comic together called Endomortis, more on that soon!

I am currently a postdoc at Uni-Münster in the Arithmetic and Homotopy Theory Working Group lead by Thomas Nikolaus and Christopher Deninger.

Before that, I graduated from George Mason University at 16 with a B.S. in Computational Physics, and accepted the Thiel Fellowship in 2014 to develop medical technology and study mathematics under my mentor, Edward Frenkel. I graduated with my Master’s degree from UChicago working with Peter May and Kazuya Kato (加藤 和也), and with my PhD from Northwestern working with Paul Goerss.

Here’s a recent interview I did as part of On a Tangent: Voices of Mathematics Muenster: How an Inventor becomes a Mathematican.

Contact me

Curiosity is welcome: fractalcows@gmail.com

My work email: cray@uni-muenster.de

If you are interested in my research mathematics, here are some fun papers of mine.

Research publications:

• Automorphisms of Abelian Varieties and Principal Polarizations joint with D. Lee; Rendiconti del Circolo Matematico di Palermo Series 2, Volume 71, pages 483–494, 2022 arxiv
• Towards Directed Collapsibility joint with R. Belton, R. Brooks, S. Ebli, L. Fajstrup, B. T. Fasy, N. Sanderson, E. Vidaurre; Advances in Mathematical Sciences, Volume 21, pages 255–271, 2020 arxiv

Research preprints:

A Global Crystalline Period Map joint with M. Neaton and A. Pieper

In progress:

Zeta Functions in Homotopy Theory:

• Riemann Roch for Rademeister Torsion in K-theory and L-Theory
• L-genera and Localizations in K-theory; joint with Daniel Berwick-Evans, Natalia Pacheco-Tallaj
• Syntomic cohomology of ring spectra and a \( T(h) \)-local zeta function; joint with Gabe Angelini-Knoll
• All Bernoulli Numbers in Homotopy Theory Are Shifts: Connecting Kevaire-Milnor to Quillen-Lichtenbaum using the compatibility of \( K(\mathbb{S}) \) and \( L_{K(1)}K(\mathbb{Z}) \) (on hiatus)

Moduli Stacks of Curves in Homotopy Theory: My thesis attempted to resolve a 40 year old conjecture, and involves a lot of parts. To make it digestible, I have broken it up into 3 parts which are forthcoming.

• (Thesis Paper 1) A Walk Through a Garden: Criterion for Modeling Groups Acting on Stacks (Especially the Lubin-Tate Action)
• (Thesis Paper 2) Squirming Jewels: Modelling the Lubin-Tate action with Ramified Families of Curves for \( h = p-1 \)

• (Thesis Paper 3) Writhing Jewels: A Conjectural Description of the Lubin-Tate Action via Ramified Families of Curves for \( h = p^{k-1}(p-1) \)

• The homotopy groups of \( E_6^{hC_9} \) and the odd primary Kevaire invariant; joint with E. Belmont
• The Eigenvalues of Frobenius of Artin-Schreier-Witt Curves are Gauss Sums (New Families of Newton Strata in the Torelli Locus)

Jacquet-Langlands and Homotopy Theory:

• Transchromatic Splitting Conjecture; joint with many.

Old and likely dead:

• Covers of the Octahedron; joint with D. Lee
• Duality resolutions for general linear groups; joint with E. Belmont, P. VanKoughnett

Expository writing:

• Here is a 4 page summary of my work as a graduate student for a general audience, including original illustrations.

• Using Automorphism Groups of Curves to Control the Slopes of their Jacobians

• (Coming Soon) K-theoretic Tate Poutou Duality

• (Coming Soon) Zeta-Functions and THH

• Geometry for Prime Addicts Background on p-adic geometry toward proving the Monodromy Weight conjecture.
• The Hecke Orbit Conjecture and Homotopy Theory Explaining that the stabilizer of the Hecke Action is the Morvava Stabilizer Group.

• An Overview of the Classic Theory of P-Divisible Groups (Published in Oberwolfach Proceedings)

• Fiber Bundles of Formal Disks (with A. Holeman)
• A Complete Proof of the Polynomial Ham Sandwich Theorem, Based on Gromov’s Proof

My two Master’s theses

• Calculating pi_*(tmf) at the prime 2 (An Illustrated Guide to the May Spectral Sequence)
• Models of Formal Group Laws of Every Height